Consider a tetrahedral volume element as shown in the figure below. It has three orthogonal faces areas $dA_1$, $dA_2$, and $dA_3$, and with normals $\hat{a}$, $\hat{c}$ and $\hat{g}$, respectively. (The symbols for the unit normals were chosen because I could not find a quick and easy way to write $\hat{b}$ while creating this figure. You can call them $\hat{a}$, $\hat{b}$ and $\hat{c}$ as is done in Batchelor’s book.)
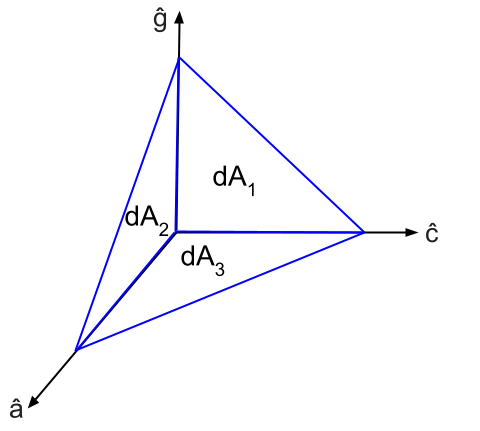
The fourth face has an area $dA$ and a normal $\hat{n}$ pointing out of the volume element. For the orthogonal faces, the outward normals are in directions, $-\hat{a}$, $-\hat{c}$ and $-\hat{g}$, respectively. The sum of the surface forces on the fluid element is therefore given by, \(\vec{\Sigma}(\hat{n})dA+\vec{\Sigma}(-\hat{a})dA_1+\vec{\Sigma}(-\hat{c})dA_2+\vec{\Sigma}(-\hat{g})dA_3\\ = \vec{\Sigma}(\hat{n})dA-\vec{\Sigma}(\hat{a})dA_1-\vec{\Sigma}(\hat{c})dA_2-\vec{\Sigma}(\hat{g})dA_3.\)
It is clear that $dA_1$ is the projection of $dA\hat{n}$ on $\hat{a}$. Therefore, $dA_1=dA\hat{n}\cdot\hat{a}$. Similarly, $dA_2=dA\hat{n}\cdot\hat{c}$ and $dA_3=dA\hat{n}\cdot\hat{g}$. Thus, the sum of the surface forces on the fluid element can be simplified to,
\[\left(\vec{\Sigma}(\hat{n}) -\vec{\Sigma}(\hat{a})\hat{a}\cdot\hat{n} -\vec{\Sigma}(\hat{c})\hat{c}\cdot\hat{n} -\vec{\Sigma}(\hat{g})\hat{g}\cdot\hat{n} \right)dA\]Now, for the volume element, writing Newton’s second law, we get, \(\rho dV\times \text{acceleration} = (\text{sum of bulk forces})+(\text{sum of surface forces})\)
The sum of bulk forces is proportional to $dV$ but the sum of surface forces is proportional to $dA$. As the volume element is made arbitrarily small, we get an inconsistency, i.e., the left hand side of this equation become negligible compared to the sum of surface forces. This means that the net surface force must vanish. Thus, we get,
\[\vec{\Sigma}(\hat{n}) =\vec{\Sigma}(\hat{a})\hat{a}\cdot\hat{n} +\vec{\Sigma}(\hat{c})\hat{c}\cdot\hat{n} +\vec{\Sigma}(\hat{g})\hat{g}\cdot\hat{n}\]The $i$\textsuperscript{th} component of $\vec{\Sigma}$ is therefore given by,
\[\Sigma_i(\hat{n}) =\left( \Sigma_i(\hat{a})a_j +\Sigma_i(\hat{c})c_j +\Sigma_i(\hat{g})g_j \right)n_j\]where we have also expanded the dot products and used Einstein’s summation convention. Now, since $\hat{n}$ and $\vec{\Sigma}$ are not dependent on the choice of the orthogonal faces used in the above treatment, $\left( \Sigma_i(\hat{a})a_j +\Sigma_i(\hat{c})c_j +\Sigma_i(\hat{g})g_j \right)$ must be independent of $\hat{a}$, $\hat{c}$ and $\hat{g}$ and must be the $(i,j)$ component of some second rank tensor (here, a $3\times3$ matrix). That is,
\[\Sigma_i(\hat{n}) =\sigma_{ij}n_j.\]Here, $\sigma_{ij}(\vec{x},t)$ represents the $(i,j)$ component of the local stress tensor.
The Stress Tensor is Symmetric
Let us try to show that the stress tensor is a symmetric tensor. The moment due to surface forces is given by,
\[\int \vec{r}\times\vec{dF}^{surface}.\]The $i$-th component of the moment is,
\[\int \epsilon_{ijk}r_jdF^{surface}_k\\ =\int \epsilon_{ijk}r_j\sigma_{kl}n_l dA\\ =\int \epsilon_{ijk}\frac{\partial r_j\sigma_{kl}}{\partial r_l}dV\\ =\int \epsilon_{ijk}\left(\delta_{jl}\sigma_{kl}+r_j\frac{\partial(\sigma_{kl})}{\partial r_l}\right)dV\\ =\int \epsilon_{ijk}\left(\sigma_{kj}+r_j\frac{\partial(\sigma_{kl})}{\partial r_l}\right)dV\]For an arbitrarily small volume, $\Delta V$, the first term of this integral is proportional to $\Delta V$ and the second term has an extra factor of the linear size and is therefore proportional to $\Delta V^{4/3}$. The net moment must be proportional $\Delta V^{4/3}$ and the first term must identically vanish. Thus,
\[\epsilon_{ijk}\sigma_{kj}=0.\]For $i=1$, we get, $\sigma_{32}-\sigma_{23}=0$. Similarly, going through the other values of $i$, we get, $\sigma_{ij}=\sigma_{ji}$.
The diagonal components of the shear stress tensor are the normal stresses and in simple isotropic situations their values are equal to the negative of the pressure in the fluid. The off-diagonal components represent tangential stresses or shear stresses.
The principal axes of the stress tensor are the set of orthogonal axes for which the shear stresses are all zero. The normal stresses are then called the principal stresses.