Classical gas
A classical gas is a system of classical identical particles. Classical identical particles have the following important properties.
- They are distinguishable, i.e., we can, in principle, follow each particle as the system evolves.
- Any number of particles can occupy a given single particle state.
- There is no restriction if two particles in the system are interchanged. (We will see that this is not true for quantum particles.)
Derivation of the Maxwell-Boltzmann distribution law
In this derivation, we will work in the microcanonical ensemble.
An alternate derivation that uses the canonical ensemble can be found in the book by Reif (Fundamentals of Statistical and Thermal Physics). The approach here is similar to those in the books by Huang (Statistical Mechanics) and by Chattopadhyay and Rakshit (Quantum Mechanics, Statistical Mechanics and Solid State Physics)
Consider a system with $N$ identical classical particles. These fill up $K$ cells in phase space.
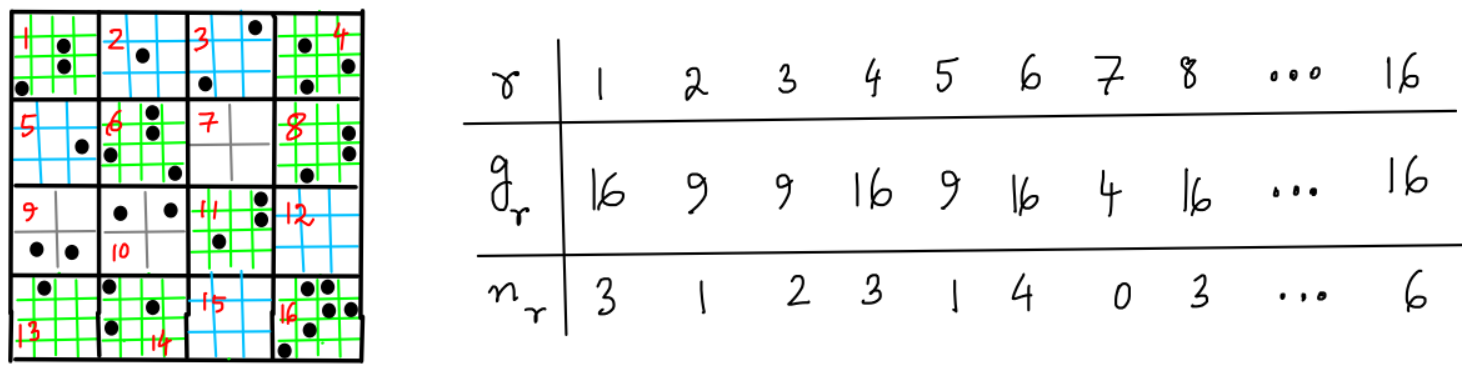
Let $\epsilon_r$ be the energy of the $r^\sf{th}$ cell. Also, let $g_r$ denote the degeneracy of the $r^\sf{th}$ cell, i.e., the number of single particle states in the $r^\sf{th}$ cell. We now impose the microcanonical constraint, i.e., we only consider microstates at a fixed value of the total energy and at a fixed value of the total number of particles.
\[\sum_rn_r=N,~\sum_rn_r\epsilon_r=E\]A distribution $R$ is specified using the number of particles occupying each of the $K$ cells in phase space. That is, $R\equiv\lbrace n_1,n_2,\dots,n_K\rbrace$. The number of microstates which correspond to the distribution $R$ is given by,
\[\Omega_R=\frac{N!}{n_1!n_2!\dots n_K!}g_1^{n_1}g_2^{n_2}\cdots g_K^{n_K}.\]This expression can be understood as follows. A microstate can be partly specified using an ordered list whose each element is an integer from 1 to $K$. The $n^\sf{th}$ element of this list specifies the cell in phase space which the $n^\sf{th}$ particle occupies. This list can be shuffled without changing the distribution $R$. In addition, the number $r$ in the list can be written in $g_r$ different colours, specifying which of the $g_r$ degenerate single particle states which the $n^\sf{th}$ particle chooses to occupy.
Our next step is to maximize $\Omega_R$ subject to the constraints due to the microcanonical treatment. Instead of working directly with $\Omega_R$, it is easier to maximize $\ln \Omega_R$. These are equivalent in the thermodynamic limit ($N\gg1$).
\[\ln\Omega_R=\ln N!-\sum_r\ln n_r!+\sum_rn_r\ln g_r\]Stirling’s Approximation: For $x\gg1$,
\[x!\sim\sqrt{2\pi x}\ x^xe^{-x},\\ \Rightarrow \ln x!\sim x\ln x -x.\]Note that in each of the the above two lines, there is a correction term which becomes negligible in comparison to the term on the right hand side when $x$ is made large compared to one. It is easier to understand the second expression than the first one.
\[\ln x!=\ln\prod_{n=1}^x n=\sum_{n=1}^x\ln n\sim\int_1^x\ln n\ dn\sim x\ln x -x.\]Look at the table below to see how good these approximations are.
$x$ $x!$ $\sqrt{2\pi x}\ x^xe^{-x}$ $\ln x!$ $x\ln x-x$ $\frac{\delta x!}{x!}$ $\frac{\delta (\ln x!)}{\ln x!}$ 2 2 1.919 0.6931 -0.6137 0.04 1.9 4 24 23.51 3.178 1.545 0.021 0.51 8 4.032e+04 3.99e+04 10.6 8.636 0.01 0.19 16 2.092e+13 2.081e+13 30.67 28.36 0.0052 0.075 32 2.631e+35 2.624e+35 81.56 78.9 0.0026 0.033 64 1.269e+89 1.267e+89 205.2 202.2 0.0013 0.015 128 3.856e+215 3.854e+215 496.4 493.1 0.00065 0.0067 256 Too big Too big 1167 1164 $-$ 0.0032 512 Too big Too big 2686 2682 $-$ 0.0015 1024 Too big Too big 6078 6074 $-$ 0.00072
Thus,
\[\ln\Omega_R\sim\ln N!-\sum_r(n_r\ln n_r-n_r)+\sum_rn_r\ln g_r\]Using Lagrange multipliers $\alpha$ and $\beta$ for the two constraints, we get at the maximum of $\ln\Omega_R$,
\[\Big[\delta\ln\Omega_R-\alpha\delta\sum_r n_r-\beta\delta\sum_r n_r\epsilon_r\Big]_{\lbrace n_r\rbrace=\lbrace \bar{n}_r\rbrace},\]where $\bar{n}_r$ are the occupation numbers which correspond to the maximum of $\ln\Omega_R$. Thus,
\[\sum_r\Big[-\ln\bar{n}_r+\ln g_r-\alpha-\beta\epsilon_r\Big]\delta n_r=0.\]The Lagrange multipliers are chosen such that the variations of $\lbrace n_r\rbrace$ around the maximum become independent. This means that the expression in the square brackets in the above equation, must be zero, i.e.,
\[-\ln\bar{n}_r+\ln g_r-\alpha-\beta\epsilon_r=0\ \Rightarrow\ \bar{n}_r=g_re^{-\alpha-\beta\epsilon_r}.\]The values of the constants $\alpha$ and $\beta$, can be obtained using the constraints. Therefore, the fraction of filled states at energy $\epsilon_r$, $\frac{n_r}{g_r}$ is proportional to $e^{-\beta\epsilon_r}$. This is the Maxwell-Boltzmann distribution law.
Quantum Gases
Identical quantum particles are also indistinguishable, i.e., if there are more than two particles, then it is impossible to distinguish between two states which differ only by one particle exchange. This results in two possibilities. Consider a two-particle quantum state in which one particle has spin $s_1$ and is located at $\vec{x}_1$ and another identical particle which has spin $s_2$ and is at $\vec{x}_2$. When we interchange these two particles, their joint wavefunction can change at most by a phase. If we perform this interchange again, we should pick up the same phase again. However, since we are back at our starting state, the square of the phase we pick up must be one, i.e., the phase itself can be $\pm1$. For a pair of identical bosons,
\[\psi_{s_1s_2}\left(\vec{x}_1,\vec{x}_2\right)=\psi_{s_2s_1}\left(\vec{x}_2,\vec{x}_1\right).\]For a pair of identical fermions,
\[\psi_{s_1s_2}\left(\vec{x}_1,\vec{x}_2\right)=-\psi_{s_2s_1}\left(\vec{x}_2,\vec{x}_1\right).\]This relation for fermions has an interesting consequence. If there are two identical particles with the same spin and at the same location, then their joint wavefunction is the negative of itself, i.e., it must be zero. Thus, such a state is not allowed (has zero probability). This is Pauli’s exclusion principle. Two identical fermions cannot occupy the same single particle state.
According to the spin-statistics theorem,
- particles with integer spins (in units of $\hbar$) are bosons, and,
- those with half-integer spins (odd multiple of $\frac{1}{2}$) are fermions.
Example: Two identical particles occupying three single particle states.
If the particles are classical particles (obey MB statistics), then we can label the particles. Calling the particles A and B, the following table lists the nine possible microstates of the system.
State 1 AB - - - B A - A B State 2 - AB - A - B B - A State 3 - - AB B A - A B - When we have quantum particles, we can no longer distinguish them. We call both the particles by the same name A. On replacing B with A in the above table, the last three columns become repetitions of the previous three and must be omitted. For bosons, we therefore have the following six microstates.
State 1 AA - - - A A State 2 - AA - A - A State 3 - - AA A A - For fermions, there is the additional requirement of Pauli’s exclusion principle which disallows the first three columns. Thus, for fermions, there are only three possible microstates.
State 1 - A A State 2 A - A State 3 A A -
Derivation of the Bose-Einstein and Fermi-Dirac distribution laws
We follow a treatment similar to the one we discussed for the gas of classical particles. For a gas of identical bosons, any number of particles can occupy a given single particle state (as was the case with classical identical particles). For a gas of identical fermions, however, not more than one particle can occupy a given single particle state.
Let us now focus on a system with $N$ bosons. As before, these fill up $K$ cells in phase space with $\epsilon_r$ denoting the energy of the $r^\sf{th}$ cell. The degeneracy of the $r^\sf{th}$ cell is denoted by $g_r$. We work in the microcanonical ensemble, i.e., we only consider microstates at a fixed value of the total energy and a fixed total number of particles.
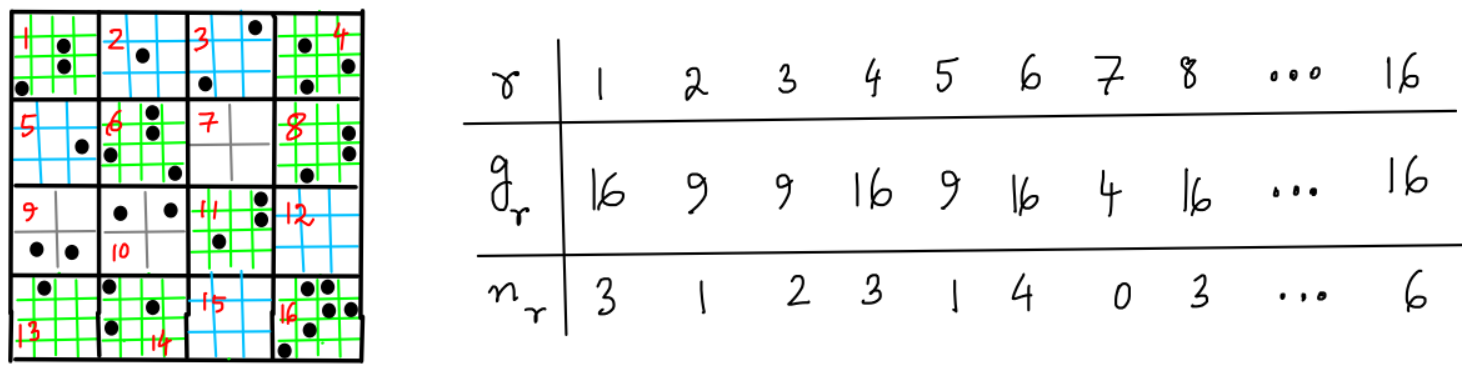
As before, a distribution $R$ is specified using the number of particles occupying the $K$ cells in phase space. That is, $R\equiv\lbrace n_1,n_2,\dots,n_K\rbrace$. The number of microstates which correspond to the distribution $R$ is now just given by,
\[\Omega_R=\omega_1\omega_2\cdots\omega_K,\]where $\omega_r$ denotes the number of ways of filling $g_r$ single particle states with $n_r$ indistinguishable particles.
This should remind you of the combinatorics problem from classes 11-12 in which you were asked to calculate the number of ways of distributing 15 identical chocolates among 20 students.
The answer is the same as the number of ways of arranging $n_r$ dots and $g_r-1$ partitions (vertical lines). In a particular arrangement, e.g.,
\[\bullet \bullet \Big| \bullet \bullet \bullet \Big| \bullet \bullet \Big| \bullet \cdots \bullet \Big| \bullet \bullet \bullet \Big| \bullet \Big| \bullet \bullet ~\bullet\]the number of dots towards the left of the first partition (2 above) denotes the number of particles filling up the first single particle state, the number of dots towards the right of the last partition (3 above) denotes the number of particles filling up the last single particle state, and, the number of dots between the $(i-1)^\sf{th}$ and the $i^\sf{th}$ partitions denotes the number of particles filling up the $i^\sf{th}$ single particle state (the number of chocolates which the $i^\sf{th}$ student gets). Therefore,
\[\omega_r=\frac{(n_r+g_r-1)!}{n_r!(g_r-1)!}.\]Thus, using Stirling’s approximation,
\[\ln\Omega_R\sim\sum_r[(n_r+g_r-1)\ln(n_r+g_r-1)-(n_r+g_r-1)-n_r\ln n_r+n_r-(g_r-1)\ln(g_r-1)+g_r-1].\]As before, using Lagrange multipliers $\alpha$ and $\beta$ to enforce the two constraints, the distrubution $\lbrace\bar{n}_r\rbrace$ which maximizes $\ln\Omega_R$ satisfies,
\[\sum_r[\ln(\bar{n}_r+g_r-1)+1-1-\ln\bar{n}_r-1+1-\alpha-\beta\epsilon_r]\delta n_r=0,\]Since $\bar{n}_r\gg1$, we get,
\[\frac{\bar{n}_r}{g_r}=\frac{1}{e^{\alpha+\beta\epsilon_r}-1}.\]If $g_r=1$, then,
\[\bar{n}_r=\frac{1}{e^{\alpha+\beta\epsilon_r}-1}.\]The values of the Lagrange multipliers, $\alpha$ and $\beta$ are obtained from the constraints.
\[\alpha=-\beta\mu\mbox{, and, }\beta=\frac{1}{k_BT},\]where $T$ is the absolute temperature and $\mu$ the chemical potential. Using these, we get,
\[\bar{n}_r=\frac{1}{e^{\beta(\epsilon_r-\mu)}-1}.\]This is the Bose-Einstein distribution law. From this equation, it is clear that $\bar{n}_r>0$ only when $\epsilon_r>\mu$ and it diverges for $\epsilon_r=\mu$. We will discuss these issues in details later.
We will now focus on a system with $N$ fermions. Again, let these fill up $K$ cells in phase space with $\epsilon_r$ denoting the energy of the $r^\sf{th}$ cell. As before, the degeneracy of the $r^\sf{th}$ cell is denoted by $g_r$. We work in the microcanonical ensemble, i.e., we only consider microstates at a fixed value of the total energy and a fixed total number of particles.
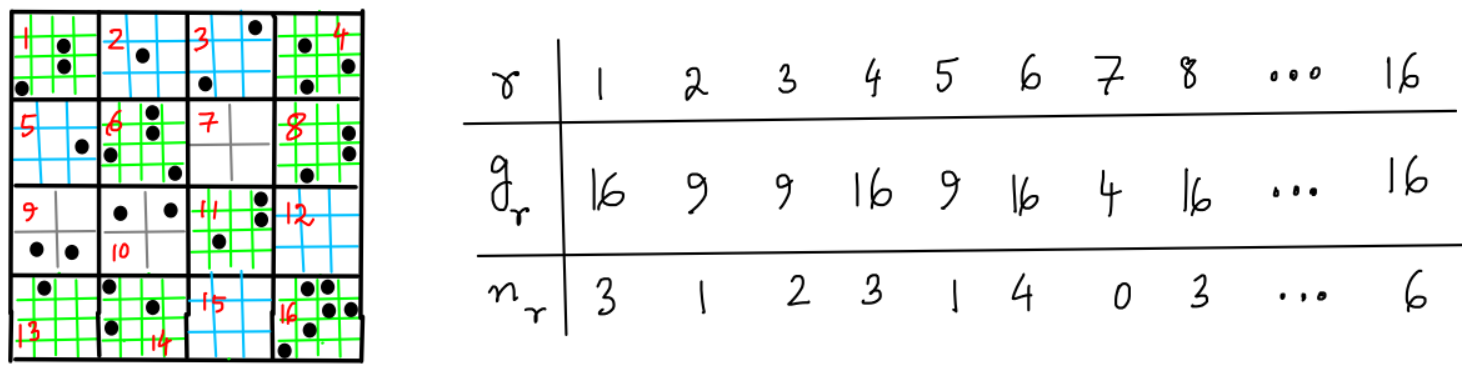
As before, a distribution $R$ is specified using the number of particles occupying the $K$ cells in phase space. That is, $R\equiv\lbrace n_1,n_2,\dots,n_K\rbrace$. The number of microstates which correspond to the distribution $R$ is now just given by,
\[\Omega_R=\omega_1\omega_2\cdots\omega_K,\]where for fermions, $\omega_r$ denotes the number of ways of choosing the $n_r$ single particle states which the fermions occupy, from the $g_r$ available states. Thus, $\omega_r$ is simply given by,
\[\omega_r=\left(\begin{array}{c}g_r\\n_r\end{array}\right)=\frac{g_r!}{n_r!(g_r-n_r)!}.\]Thus, using Stirling’s approximation,
\[\ln\omega_r=\ln g_r!-n_r\ln n_r+n_r-(g_r-n_r)\ln(g_r-n_r)+g_r-n_r.\] \[\Rightarrow \ln\Omega_R\sim\sum_r[-n_r\ln n_r-(g_r-n_r)\ln(g_r-n_r)]+constant.\]As before, using Lagrange multipliers $\alpha$ and $\beta$ to enforce the two constraints, the distrubution $\lbrace\bar{n}_r\rbrace$ which maximizes $\ln\Omega_R$ satisfies,
\[\sum_r[-\ln \bar{n}_r-1+1+\ln(g_r-\bar{n}_r)-\alpha-\beta\epsilon_r]\delta n_r=0,\]Thus,
\[\frac{\bar{n}_r}{g_r}=\frac{1}{e^{\alpha+\beta\epsilon_r}+1}.\]If $g_r=1$, then,
\[\bar{n}_r=\frac{1}{e^{\alpha+\beta\epsilon_r}+1}.\]As before, the values of the Lagrange multipliers are obtained using the constraint equations.
\[\alpha=-\beta\mu\mbox{, and, }\beta=\frac{1}{k_BT}.\]Thus,
\[\bar{n}_r=\frac{1}{e^{\beta(\epsilon_r-\mu)}+1}.\]This is the Fermi-Dirac distribution law. At $T=0$, i.e., $\beta\to\infty$, the above formula looks like a step function. The value of the chemical potential at absolute zero is known as the Fermi energy and is denoted by $\epsilon_F$. At $T=0$, all states whose energies are below $\epsilon_F$ are occupied and all states with energies higher than $\epsilon_F$ are empty. As the temperature increases, the step smoothens and the width of the band of energies for which $\bar{n}_r$ is neither one nor zero is of the order of $k_BT$.